(脚注1)
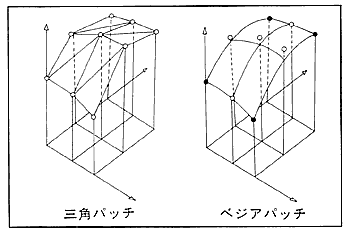
三角パッチ:隣接する3点を結んだ三角形をつないでいく。図のように9点で8つの三角形ができ、計算が簡単であるが、つなぎ目が角張る。
ベジアパッチ:3点ずつをベジア曲線で近似する。図のように9点で4つのベジア曲線で囲まれた一つの曲面ができ、面のつなぎ目が目立たない。黒丸はベジア曲線上にあり、白丸は曲率を決定するために用いられる。
(脚注2)
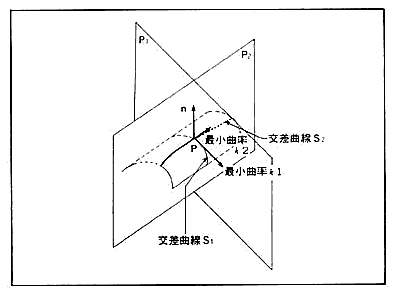
図により面曲率の算出法を述べる。任意曲面上の点Pにおける法線をn、接線をtiとし、nとtiを含む法平面Piを考える。曲面とPiの交差曲線の曲率(法曲率と言う)の中で、最大曲率κ1(交差曲線S1の曲率)、最小曲率κ2(交差曲線S2の曲率)が得られれば、Pにおける曲面の局所形状を微分幾何学に基づいて正確に記述することができる。無数の法曲率を計算するのは不可能であるが、異なる4方向の法曲率を求め、計算式に代入することにより、一意にκ1、κ2を決定できる。